1. Prérequis
Ce tutoriel s'adresse aux étudiants de master topologie algébrique. Afin de pourvoir lire et comprendre ce tutoriel, vous devez avoir le niveau requis notamment les notions d'homologie simpliciale.
2. A propos de la bibliothèque simplicial
La bibliothèque simplicial est née suite à l'usage de la topologie algébrique dans le contexte de réseaux de capteurs sans fil, pour résoudre des problèmes tels que le suivi de cible et l'estimation de la qualité d'ajustement des interpolations à partir d'observations isolées. Sa principale contribution est de représenter et de manipuler des complexes simpliciaux, des structures topologiques décrivant des espaces construits à partir de cellules.
Ce tutoriel se concentrera sur l'utilisation de la bibliothèque simplicial Python pour créer et manipuler des complexes simpliciaux, et sur ce qui peut être fait pour les analyser. Nous allons voir les opérations de base. Pour plus de détails consultez la doc officielle de la bibliothèque simplicial: https://simplicial.readthedocs.io/en/latest/.
Documentation: https://simplicial.readthedocs.io/en/latest/
3. Installation de la bibliothèque 'simplicial'
3.1 Installation sous Windows
La bibliothèque simplicial s'installe d'une façon assez simple via l'utilitaire pip:
|
1 |
pip install simplicial |
3.2 Installation sous linux
l'installation sous linux est identique à celle de Windows
4. Construire un complexe simplicial
Avec la classe SimplicialComplex intégrée au sein de la bibliothèque simplicial, on peut facilement créer un objet complexe simplicial via une instanciation de la classe:
|
1 2 3 4 5 |
# importation de la bibliothèque simplicial from simplicial import * # création d'un objet d'instance c = SimplicialComplex() |
Le complexe 'c' ainsi crée est vide, car il ne contient aucun simplexe. Nous pouvons donc lui ajouter des simplexes. Commençons par ajouter des simplexe de dimension 0 ( des points):
|
1 2 3 4 5 6 |
# ajouter un simplex avec un nom généré automatiquement s1 = c.addSimplex() # ajouter des simplexes avec des identifiants spécifiques s2 = c.addSimplex(id = 2) s3 = c.addSimplex(id = 3) |
Code complet:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# importation de la bibliothèque simplicial from simplicial import * # création d'un objet d'instance c = SimplicialComplex() # ajouter un simplex avec un nom généré automatiquement s1 = c.addSimplex() # ajouter des simplexes avec des identifiants spécifiques s2 = c.addSimplex(id = 2) s3 = c.addSimplex(id = 3) print(s1) # output: 0d0 print(s2) # output: 2 print(s3) # output: 3 |
Ces lignes ajoutent toutes des 0-simplexes (des points) au complexe. La méthode SimplicialComplex.addSimplex() renvoie le nom du simplexe ajouté, qui sera soit celui donné dans son argument id, soit un nom synthétique si aucun nom n'est donné explicitement. Nous pouvons alors construire des 1-simplexes (des segments de droites) en fournissant deux 0-simplexes comme extrémités :
|
1 2 |
# ajout du segment [2 , 3] au complexe simplicial l23 = c.addSimplex(fs = [ 2, 3 ]) |
Si on souhaite afficher la structure qui compose le complexe simpliciale, on utilise la méthode simplices() de la classe SimplicialComplex:
|
1 2 3 4 5 6 7 8 9 |
""" on conserve le code ci-dessus .... """ print(c.simplices()) # output: ['0d0', 2, 3, 4, '1d1'] |
5. Suppression de simplexes
Les simplexes peuvent être supprimés d'un complexe aisement avec la méthode deleteSimplex():
|
1 |
c.deleteSimplex(s5) |
Le même effet peut être obtenu via une interface opérateur :
|
1 |
del c[s5] |
Dans les deux cas, la suppression de s5 supprimerait une partie de la base du triangle tabc ainsi que l'extrémité de deux de ses faces, et ces simplexes seront automatiquement supprimés également.
Ramarque
Supprimer un simplexe supprimera tous les simplexes dont il fait partie. Cela implique que la suppression d'un simplexe peut supprimer d'autres simplexes d'ordres supérieurs à lui-même. Les simplexes exacts supprimés peuvent être trouvés en utilisant SimplicialComplex.partOf().
6. Caractéristiques Euler
Contrairement aux opérations de navigation et d'interrogation d'un complexe qui sont locales, à partir d'un seul simplexe, les opérations d'analyse sont généralement globales, indiquant quelque chose sur les propriétés de l'ensemble du complexe. Souvent, chaque propriété est un invariant topologique d'un complexe, à l'abri des changements "sans importance".
La caractéristique d'Euler d'un complexe est définie comme suit :
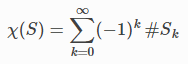
où #Sk représente le nombre de k-simplexes dans S. Plus intuitivement, on calcule "points moins droites plus triangles moins tétraèdres plus…" et ainsi de suite, pour tous les ordres du complexe. La bibliothèque 'simplicial' nous donne directement la caractéristique d'Euler :
|
1 |
chEuler = c.eulerCharacteristic() |
7. Homologie et nombres de Betti
L'idée d'homologie est de détecter des « trous de différentes dimensions » dans un complexe. L'homologie fonctionne en créant des groupes qui reflètent la structure des trous à chaque ordre différent de simplexe dans le complexe. simplicial inclut une implémentation particulière de l'homologie simpliciale qui peut être utilisée pour effectuer de telles analyses.
L'interface la plus simple est utilisée pour calculer les nombres de Betti d'un complexe, renvoyant un dict pour chaque commande:
|
1 |
bs = c.bettiNumbers() |
On peut éventuellement fournir une liste des dimensions.
Étant donné un ensemble de k-simplices, la frontière est l'ensemble de (k - 1)-simplices qui apparaissent « non connectés » à l'arête ; La frontière d'un simple 1-simple, par exemple, est l'ensemble de deux 0-simplices qui sont ses extrémités ; un triangle de 1-simplices n'a pas de bord. On peut calculer directement les frontières :
|
1 |
bs = c.boundary([ l12, l23 ]) |
Code complet:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# importation de la bibliothèque simplicial from simplicial import * # création d'un objet d'instance c = SimplicialComplex() # ajouter un simplex avec un nom généré automatiquement s1 = c.addSimplex() # ajouter des simplexes avec des identifiants spécifiques s2 = c.addSimplex(id = 2) s3 = c.addSimplex(id = 3) s4 = c.addSimplex(id = 4) l23 = c.addSimplex(fs = [ 2, 3 ] ) l12 = c.addSimplex(fs = [ s1, 2 ]) l31 = c.addSimplex(fs = [ s1, 3 ]) # create the triangle t123 = c.addSimplex(fs = [l12, l23, l31]) # Caractéristique d'Euler print(c.eulerCharacteristic()) # output: 2 # nombres de Betti print(c.bettiNumbers()) # output: {0: 2, 1: 0, 2: 0} # boundary print(c.boundary([ l12, l23 ])) # output: {3, '0d0'} |
Younes Derfoufi
CRMEF OUJDA
Leave a Reply
You must be logged in to post a comment.