admin

Homologie Simpliciale En Python: Bibiliothèque ‘simplicial’

Published November 27, 2022

Contenu du cours

Prérequis
A propos de la bibliothèque 'simplicial'
Installation de la bibliothèque 'simplicial'
Construire un complexe simplicial
Suppression de simplexes
Caractéristiques Euler
Homologie et nombres de Betti

1. Prérequis

Ce tutoriel s'adresse aux étudiants de master topologie algébrique. Afin de pourvoir lire et comprendre ce tutoriel, vous devez avoir le niveau requis notamment les notions d'homologie simpliciale.

2. A propos de la bibliothèque simplicial

La bibliothèque simplicial est née suite à l'usage de la topologie algébrique dans le contexte de réseaux de capteurs sans fil, pour résoudre des problèmes tels que le suivi de cible et l'estimation de la qualité d'ajustement des interpolations à partir d'observations isolées. Sa principale contribution est de représenter et de manipuler des complexes simpliciaux, des structures topologiques décrivant des espaces construits à partir de cellules.
Ce tutoriel se concentrera sur l'utilisation de la bibliothèque simplicial Python pour créer et manipuler des complexes simpliciaux, et sur ce qui peut être fait pour les analyser. Nous allons voir les opérations de base. Pour plus de détails consultez la doc officielle de la bibliothèque simplicial: https://simplicial.readthedocs.io/en/latest/.
Documentation: https://simplicial.readthedocs.io/en/latest/

3. Installation de la bibliothèque 'simplicial'

3.1 Installation sous Windows

La bibliothèque simplicial s'installe d'une façon assez simple via l'utilitaire pip:

pip install simplicial

1	pip install simplicial

3.2 Installation sous linux

l'installation sous linux est identique à celle de Windows

4. Construire un complexe simplicial

Avec la classe SimplicialComplex intégrée au sein de la bibliothèque simplicial, on peut facilement créer un objet complexe simplicial via une instanciation de la classe:

# importation de la bibliothèque simplicial
from simplicial import *

# création d'un objet d'instance
c = SimplicialComplex()

1

2

3

4

5

# importation de la bibliothèque simplicial

from simplicial import *

# création d'un objet d'instance

c = SimplicialComplex()

Le complexe 'c' ainsi crée est vide, car il ne contient aucun simplexe. Nous pouvons donc lui ajouter des simplexes. Commençons par ajouter des simplexe de dimension 0 ( des points):

# ajouter un simplex avec un nom généré automatiquement
s1 = c.addSimplex()

# ajouter des simplexes avec des identifiants spécifiques
s2 = c.addSimplex(id = 2)
s3 = c.addSimplex(id = 3)

1

2

3

4

5

6

# ajouter un simplex avec un nom généré automatiquement

s1 = c.addSimplex()

# ajouter des simplexes avec des identifiants spécifiques

s2 = c.addSimplex(id = 2)

s3 = c.addSimplex(id = 3)

Code complet:

# importation de la bibliothèque simplicial
from simplicial import *

# création d'un objet d'instance
c = SimplicialComplex()
# ajouter un simplex avec un nom généré automatiquement
s1 = c.addSimplex()

# ajouter des simplexes avec des identifiants spécifiques
s2 = c.addSimplex(id = 2)
s3 = c.addSimplex(id = 3)

print(s1) # output: 0d0
print(s2) # output: 2
print(s3) # output: 3

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

# importation de la bibliothèque simplicial

from simplicial import *

# création d'un objet d'instance

c = SimplicialComplex()

# ajouter un simplex avec un nom généré automatiquement

s1 = c.addSimplex()

# ajouter des simplexes avec des identifiants spécifiques

s2 = c.addSimplex(id = 2)

s3 = c.addSimplex(id = 3)

print(s1) # output: 0d0

print(s2) # output: 2

print(s3) # output: 3

Ces lignes ajoutent toutes des 0-simplexes (des points) au complexe. La méthode SimplicialComplex.addSimplex() renvoie le nom du simplexe ajouté, qui sera soit celui donné dans son argument id, soit un nom synthétique si aucun nom n'est donné explicitement. Nous pouvons alors construire des 1-simplexes (des segments de droites) en fournissant deux 0-simplexes comme extrémités :

# ajout du segment [2 , 3] au complexe simplicial
l23 = c.addSimplex(fs = [ 2, 3 ])

1 2	# ajout du segment [2 , 3] au complexe simplicial l23 = c.addSimplex(fs = [ 2, 3 ])

Si on souhaite afficher la structure qui compose le complexe simpliciale, on utilise la méthode simplices() de la classe SimplicialComplex:

"""
on 
conserve 
le code 
ci-dessus
....
"""
print(c.simplices())
# output: ['0d0', 2, 3, 4, '1d1']

1

2

3

4

5

6

7

8

9

"""

on

conserve

le code

ci-dessus

....

"""

print(c.simplices())

# output: ['0d0', 2, 3, 4, '1d1']

5. Suppression de simplexes

Les simplexes peuvent être supprimés d'un complexe aisement avec la méthode deleteSimplex():

c.deleteSimplex(s5)

1	c.deleteSimplex(s5)

Le même effet peut être obtenu via une interface opérateur :

del c[s5]

1

del c[s5]

Dans les deux cas, la suppression de s5 supprimerait une partie de la base du triangle tabc ainsi que l'extrémité de deux de ses faces, et ces simplexes seront automatiquement supprimés également.

Ramarque

Supprimer un simplexe supprimera tous les simplexes dont il fait partie. Cela implique que la suppression d'un simplexe peut supprimer d'autres simplexes d'ordres supérieurs à lui-même. Les simplexes exacts supprimés peuvent être trouvés en utilisant SimplicialComplex.partOf().

6. Caractéristiques Euler

Contrairement aux opérations de navigation et d'interrogation d'un complexe qui sont locales, à partir d'un seul simplexe, les opérations d'analyse sont généralement globales, indiquant quelque chose sur les propriétés de l'ensemble du complexe. Souvent, chaque propriété est un invariant topologique d'un complexe, à l'abri des changements "sans importance".
La caractéristique d'Euler d'un complexe est définie comme suit :

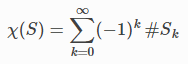
où #S_k représente le nombre de k-simplexes dans S. Plus intuitivement, on calcule "points moins droites plus triangles moins tétraèdres plus…" et ainsi de suite, pour tous les ordres du complexe. La bibliothèque 'simplicial' nous donne directement la caractéristique d'Euler :

chEuler = c.eulerCharacteristic()

1	chEuler = c.eulerCharacteristic()

7. Homologie et nombres de Betti

L'idée d'homologie est de détecter des « trous de différentes dimensions » dans un complexe. L'homologie fonctionne en créant des groupes qui reflètent la structure des trous à chaque ordre différent de simplexe dans le complexe. simplicial inclut une implémentation particulière de l'homologie simpliciale qui peut être utilisée pour effectuer de telles analyses.

L'interface la plus simple est utilisée pour calculer les nombres de Betti d'un complexe, renvoyant un dict pour chaque commande:

bs = c.bettiNumbers()

1	bs = c.bettiNumbers()

On peut éventuellement fournir une liste des dimensions.
Étant donné un ensemble de k-simplices, la frontière est l'ensemble de (k - 1)-simplices qui apparaissent « non connectés » à l'arête ; La frontière d'un simple 1-simple, par exemple, est l'ensemble de deux 0-simplices qui sont ses extrémités ; un triangle de 1-simplices n'a pas de bord. On peut calculer directement les frontières :

bs = c.boundary([ l12, l23 ])

1	bs = c.boundary([ l12, l23 ])

Code complet:

# importation de la bibliothèque simplicial
from simplicial import *

# création d'un objet d'instance
c = SimplicialComplex()
# ajouter un simplex avec un nom généré automatiquement
s1 = c.addSimplex()

# ajouter des simplexes avec des identifiants spécifiques
s2 = c.addSimplex(id = 2)
s3 = c.addSimplex(id = 3)
s4 = c.addSimplex(id = 4)

l23 = c.addSimplex(fs = [ 2, 3 ] )

l12 = c.addSimplex(fs = [ s1, 2 ])
l31 = c.addSimplex(fs = [ s1, 3 ])

# create the triangle
t123 = c.addSimplex(fs = [l12, l23, l31])

# Caractéristique d'Euler
print(c.eulerCharacteristic())
# output: 2

# nombres de Betti
print(c.bettiNumbers()) 
# output: {0: 2, 1: 0, 2: 0}

# boundary
print(c.boundary([ l12, l23 ]))
# output: {3, '0d0'}

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

# importation de la bibliothèque simplicial

from simplicial import *

# création d'un objet d'instance

c = SimplicialComplex()

# ajouter un simplex avec un nom généré automatiquement

s1 = c.addSimplex()

# ajouter des simplexes avec des identifiants spécifiques

s2 = c.addSimplex(id = 2)

s3 = c.addSimplex(id = 3)

s4 = c.addSimplex(id = 4)

l23 = c.addSimplex(fs = [ 2, 3 ] )

l12 = c.addSimplex(fs = [ s1, 2 ])

l31 = c.addSimplex(fs = [ s1, 3 ])

# create the triangle

t123 = c.addSimplex(fs = [l12, l23, l31])

# Caractéristique d'Euler

print(c.eulerCharacteristic())

# output: 2

# nombres de Betti

print(c.bettiNumbers())

# output: {0: 2, 1: 0, 2: 0}

# boundary

print(c.boundary([ l12, l23 ]))

# output: {3, '0d0'}

Younes Derfoufi
CRMEF OUJDA

Posted in Python | Leave a comment

Ecole GéToPhyMa

Published March 18, 2018

http://www.uir.ac.ma/pole/institut-des-classes-preparatoires/activites

Posted in AlgebraicTopology

A new lower bound for LS-category – Youssef Rami

Published September 3, 2017

.
.

.

Posted in AlgebraicTopology

MAAT Casablanca

Published November 4, 2016

Séminaire 26/05/2017
Programme:
9h00-10h30 : Homologie persistante; M. Jaraf.

Séminaire 12/05/2017
Programme:
8h45-10h15 : Groupe de Gottlieb (Suite); A. Zaim.

Séminaire 05/05/2017
Programme:
8h45-10h15 : Groupe de Gottlieb (Partie 1); S. Chouinguou.
10h30-12h00 : Groupe de Gottlieb (Partie 2); A. Zaim.
Séminaire 28/04/2017
Programme:
10h30-12h00 : Suite spectrale: construction par les filtrations (2); M. JARAF.

Séminaire 21/04/2017
Programme:
8h45-10h15 : Groupe de Gottlieb; S. Chouinguou.
10h30-12h00 : Suite spectrale: construction par les filtrations; M. JARAF.
Séminaire 14/04/2017
Programme: À partir de 8h45
Exposé 1: Réalisation d'un espace topologique comme Baut d'un espace (suite2); A. ZAIM.
Exposé 2: Groupe de Gottlieb; S. Chouinguou.
Séminaire 31/03/2017
Programme: À partir de 8h45
Exposé 1: Réalisation d'un espace topologique comme Baut d'un espace (suite); A. ZAIM.
Séminaire 24/03/2017
Programme: À partir de 8h45
Exposé 1: Suite spectrales II: Construction; M. JARAF
Exposé 2: Réalisation d'un espace topologique comme Baut d'un espace; A. ZAIM.
Séminaire 17/03/2017
Programme: À partir de 8h45
Exposé 1: Modèle de Baut (Suite); S. Chouinguou.
Exposé 2: Suite spectrales I: Introduction; M. JARAF
Séminaire 10/03/2017
Programme: À partir de 8h45
Exposé 1: Modèle de Baut ; S. Chouinguou.

Séminaire 03/03/2017
Programme: À partir de 8h45
Exposé 1: Modèle de Baut ; S. Chouinguou.

Séminaire 20/01/2017
Programme: À partir de 8h45
Exposé 1: Construction du Baut. (Construction de Dold & Lashos); A. Zaim
Exposé 2: Modèle Minimal du Baut; S. Chouinguou.

Posted in AlgebraicTopology

MAAT Meknès

Published November 4, 2016

Séminaire MAAT Meknès 28-11-2024

Programme:

16h30-18h30 : Topological persistence and machine learning; Ghizlane Kzizi.

Séminaire MAAT Meknès 14-11-2024

Programme:

16h00-18h00 : Stability of persistent modules; Ismail Benzaki.

Séminaire MAAT Meknès 07-11-2024

Programme:

16h00-18h00 : Decomposition of persistent modules; Ismail Benzaki.

Séminaire MAAT Meknès 31-10-2024

Programme:

16h00-18h00 : Introduction à l'analyse topologique des données (3); Ismail Benzaki.

Séminaire MAAT Meknès 24-10-2024

Programme:

16h00-18h00 : Introduction à l'analyse topologique des données (2); Ismail Benzaki.

Séminaire MAAT Meknès 17 Octobre 2024

Programme:

16h00-18h00 : Introduction à l'analyse topologique des données; Ismail Benzaki.

Séminaire MAAT Meknès 10 Octobre 2024

Programme:

16h00-17h30 : Discussions autour de l'analyse topologique des données, pespectives, programme et méthode de travail

Séminaire 02 Juin 2017

Programme:

13h30-17h30 : Suites spectrale d'une fibration (Suite); Abdelali ABOUHALI.

Séminaire 26 Mai 2017

Programme:

13h30-17h30 : Cohomologie et complexité topologique (Suite); Smail BENZAKI.

Séminaire 19 Mai 2017

Programme:

13h30-17h30 : Suites spectrale d'une fibration (Suite); Abdelali ABOUHALI.

Séminaire 12 Mai 2017

Programme:

16h30-17h30 : Suites spectrale d'une fibration; Abdelali ABOUHALI.

17H30-18H30 : Cohomologie et complexité topologique; Smail BENZAKI.

Séminaire 05 Mai 2017

Programme:

16h30-17h30 : Les suites spectrales (3); Abdelali ABOUHALI.

17H30-18H30 : Le produit cup; Youssef RAMI.

Séminaire 28 Avril 2017

Programme:

16h30-17h30 : Le produit cup; Youssef RAMI. (Reporté)

17H30-18H30 : Les suites spectrales (2); Abdelali ABOUHALI.

Séminaire 21 Avril 2017

Programme:

16h30-17h30 : On endpoints fibration; Smail BENZAKI.

17H30-18H30 : Les suites spectrales; Abdelali ABOUHALI.

Séminaire 14 Avril 2017

Programme:

16h30-17h30 : Promenade dans la complexité topologique (Suite); Azzeddine BOUDJAJ

17H30-18H30 : On endpoints fibration; Smail BENZAKI.

Séminaire 31 Mars 2017

Programme:

16h30-17h30 : Promenade dans la complexité topologique; Azzeddine BOUDJAJ

17H30-18H30 : Exemples de calcul de la complexité topologique d'un groupe; En-Feur Oulaid.

Posted in AlgebraicTopology

Association

Published May 1, 2016

Association MAAT

PV
Photos Souvenirs : Photo 1 | Photo 2 | Photo 3 |

1

Posted in AlgebraicTopology

Journal

Published April 22, 2016


www.uir.ac.ma	www.algtop.net/

Journal of Geometry & Topology

in

Physics & Mathematcis

Journal of GeToPhyMa

Are You interested : Go to https://docs.google.com/forms/d/1L3GfaL05xk6TqLUDBJNeaZDNZEQW2pdUcUmCRXPxKiU/viewform

About the journal : Journal of GeToPhyMa is a fully refereed journal covering all of geometry and topology, broadly understood.

Impartiality Statement : The purpose of Journal of GeToPhyMa is the advancement of mathematics. Editors evaluate submitted papers strictly on the basis of scientific merit with the help of peer review reports, without regard to authors' nationality, country of residence, institutional affiliation, sex, ethnic origin, or political views.

Aims and scope : The Journal of GeToPhyMa is a peer-reviewed international journal, which publishes original research papers and survey articles in all aspects of geometry and topology and their applications. Topics in detail to be covered are: Algebraic Geometry, Algebraic Topology, Homotopy Theory, Differential Geometry (including Non-commutative), Differential Topology, Low Dimensional Topology, Geometrical approaches to Dynamical Systems and Partial Differential Equations, Global Analysis and Global Riemannian Geometry, Lie Groups and Lie Algebras and their Representations, Quantum Groups and their Representations, Calculus of Variations on Manifolds, Geometrical aspects of Mathematical Physics as well as areas of interactions between topology and other disciplines.

Editorial Board & Interest Areas

Honorory editor : Jim Stasheff, University of Pennsylvania, USA

geometry, topology, and physics

Editor in chief : My Ismail Mamouni, CRMEF Rabat, Morocco

Topological robotics

Managing editors :
- M'Feddal Hilali, UIR Rabat, Morocco
- Younes Derfoufi, CRMEF Oujda, Morocco

Advisory editors :
Andrew Baker, University of Glasgow, Scotland, UK

Algebraic topology, Stable homotopy theory

Hisham Sati, University of Pittsburg, USA

Quantum theory, Interactions between geometry, topology, and physics

Antonio Viruel, University of Malaga, Spain

Homotopy Theory, Group theory and generalizations, Topological transformation groups, Lie algebras and Lie super algebras

Associate editors :
Yaël Frégier, University of Atrois Lens, France

Operads, L_infinity algebras, Poisson geometry

Urtzi Buijs, University of Malaga, Spain

Algebraic topology, rational homotopy theory, higher algebraic structures

Frank Neumann, University of Leicester, UK

Algebraic topology, Algebraic Geometry, Moduli spaces

Ittay Weiss, University of the South Pacific, Fiji Islands

General topology

Alberto Cattaneo, University of Zurich, Switzerland

Algebraic topology, Mathematical Physics

Aaron Mazel-Gee, University of California Berkeley, USA

homotopy theory, (higher) category theory, K-theory

Abdessatar Barhoumi, University of Carthage, Tunisia

Probability theory and stochastic processes

Behrooz Mashayekhy, Ferdowsi University of Mashhad, Iran

Algebraic topology, Group Theory

Najoua Gamara, El Manar University of Tunis, Tunisia and Taibah University of Al Medina, Saudia Arabia

Global analysis, analysis on manifolds

Vitaliy Kurlin, University of Durham, UK.

Low-dimensional topology, topological data analysis.

Gwyn Bellamy, University of Glasgow, Scotland, UK

Lie theory

Important Dates :

May-June-July 2016 : Form the editorial board
August-September-October 2016 : Conception of the website and online submissions system
November-December 2016 : Publicity
January 2017 : Submission opened
January 2018 (at most) : First publications

Posted in AlgebraicTopology

Soutenances

Published January 11, 2016

Nos Soutenance

2024:

Said Hamoun : Doctorat (PhD)
- Annonce officielle | Exposé de Soutenance | Thèse

2021:

Chouingou Saloua : Doctorat (PhD)
- Annonce officielle | Exposé de Soutenance | Thèse
Zaim Abdelhadi : Doctorat (PhD)
- Annonce officielle | Exposé de Soutenance
Azzeddine BOUDJAJ : Doctorat (PhD)
- Annonce officielle | Exposé de Soutenance

2020:

Mohamed Anas HILALI : Doctorat (PhD)
- Annonce officielle | Exposé de Soutenance | Thèse

2019:

Derfoufi Younes : Doctorat (PhD)
- Annonce officielle | Exposé de Soutenance | Thèse

2018:

Aaya Hassan : Doctorat (PhD)
- Annonce officielle | Exposé de Soutenance | Thèse
Ben El Krafi Badr : Doctorat (PhD)
- Annonce officielle | Exposé de Soutenance
Tarik Jawad : Doctorat (PhD)
- Annonce officielle | Exposé de Soutenance